Eigenpairs
Lecture 1 coda
January 22th, 2020
Eigenpairs
Relevant sources for background self-study
Ian Goodfellow, Yoshua Bengio and Aaron Courville:
Deep Learning MIT Press, 2016.
Jure Lescovec, Anand Rajaraman, Jeffrey D. Ullmann Mining of Massive datasets MIT Press, 2016.
Spectral Analysis
Eigenpairs
Matrix
In principle, if
In practice,
they might not be real, nor
≠0 are always costly to find.
A square matrix
A is symmetric (A=AT )x⃗ TAx⃗ ≥0 for anyx⃗
In such case its eigenvalues are non-negative:
Underlying idea, I
Eigenvectors, i.e., solutions to
describe the direction along which matrix A operates an expansion
as opposed to
rotation
deformation
Example: shear mapping
The blue line is unchanged:
an
[x,0]T eigenvectorcorresponding to
λ=1
Eigen. of user-activity matrices
Eigenvectors are always orthogonal with each other: they describe alternative directions, interpretable as topic
Eigenvalues expand one’s affiliation to a specific topic.
Simple all-pairs extraction via Numpy/LA:

Caveat: e-values come normalized:
hence multiply them by
Norms, distances etc.
Euclidean norm
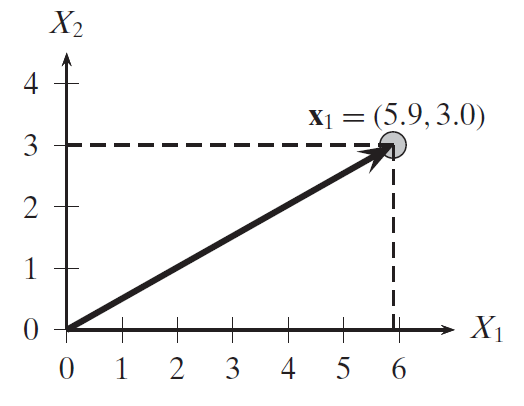
General case:
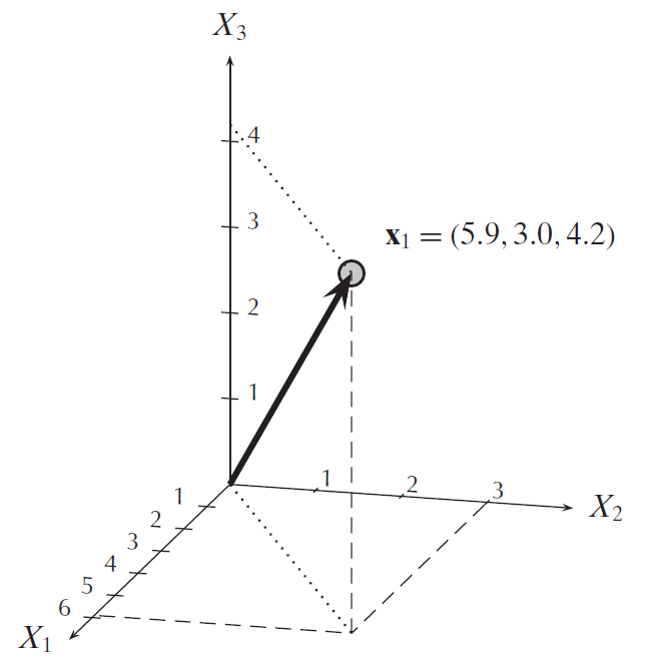
The Frobenius norm
Normalization
The unit or normalized vector of
keeps the directon
norm is set to 1.
Computing Eigenpairs
With Maths
Handbook solution: solve the equivalent
A non-zero x is associated to a solution of
In Numerical Analysis
find the
With Computer Science
At Google scale,
Ideas:
find the e-vectors first, with an iterated method.
interleave iteration with control on the expansion in value
until a fix point:
Now, eliminate the contribution of the first eigenpair:
Repeat the iteration on
